目次
Frontier Math: A Benchmark for Evaluating Advanced Mathematical Reasoning in AI
この論文は、AIの高度な数学的推論能力を評価するための新しいベンチマーク「FrontierMath」を紹介し、現在のAIモデルが解決できない難解な数学問題を提供しています。
論文:https://arxiv.org/abs/2411.04872
リポジトリ:https://github.com/epoch-research/artin_code/
以下は、LLMを用いてこの論文の内容を要約したものになります。
要約
この論文では、FrontierMathというベンチマークを紹介しています。このベンチマークは、数論や実解析から代数幾何やカテゴリー理論まで、現代数学の主要な分野を網羅する数百の独自で非常に難しい数学問題から構成されています。解決には数時間から数日を要する問題が多く、現在の最先端AIモデルは2%未満の問題しか解けないことが分かりました。FrontierMathは、AIの数学能力の進展を定量的に評価するための厳格なテストベッドを提供し、数学コミュニティの能力との大きなギャップを明らかにします。最終的に、AIシステムが研究レベルの数学を解決できる能力を持つかどうかを評価するための基準として機能します。
FrontierMathは、数百の未発表の高度な数学問題を集め、AIの数学的推論能力を評価するための新しい基準を提供することで、既存のベンチマークのデータ汚染問題を解決し、AIと人間の数学者の能力のギャップを明確に示します。
1. はじめに
1.1 背景
近年のAIシステムは、幾何学的な問題解決から組み合わせ論の研究に至るまで、高度な数学的課題に対して驚異的な能力を示しています。しかし、既存のベンチマークには限界があり、特に高校レベルや初年次の学部に偏った内容が多く、高度な数学を評価する手段が不足しています。また、データの汚染がAIモデルの評価に影響を与えることも問題視されています。
1.2 FrontierMathの導入
この課題を解決するために、新たにFrontierMathというベンチマークが開発されました。これは、数理論、代数幾何学、圏論など現代数学の主要な分野から構成された数百の難問を集めたもので、AIシステムの数学的能力を厳密に評価するための基準を提供します。
2. データ収集
2.1 問題作成の流れ
FrontierMathの問題は、60人以上の数学者の協力により開発されました。問題は独自性、自動検証可能性、推測不可性、計算可能性の4つの要件を満たす必要があります。これにより、単なるパターンマッチングでは解決できない新しい問題が作成されています。
2.2 自動検証
すべての問題は、自動的に検証可能な形式で構築されており、AIモデルが出した解をPythonオブジェクトとして保存し、検証スクリプトがその正当性を確認します。このプロセスにより、評価の効率性が向上します。
2.3 検証と品質保証
各問題は専門家による盲目的なピアレビューを経て、正確性や難易度が評価されます。これにより高品質なベンチマークが維持され、エラーのリスクが最小限に抑えられます。
3. データセットの構成
FrontierMathは、現代数学の広範な分野をカバーし、特に数論や組合せ論が多くを占めています。これにより、AIモデルの数学的能力の評価に必要な多様な問題セットが提供されています。
4. 評価
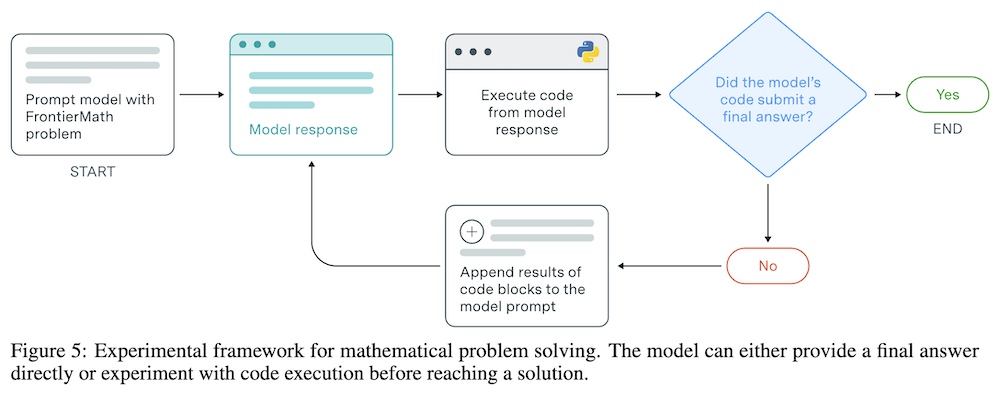
4.1 実験を通じた評価フレームワーク
AIモデルがFrontierMathの問題を解決するためのフレームワークが開発され、モデルが実験的にアプローチを検証することが可能です。このプロセスは、数学者が直面する問題解決のアプローチを模倣しています。
4.2 結果
評価結果によると、現在の主要なAIモデルは問題の2%未満しか解けず、AIの数学的能力が依然として人間の数学者と比較して大きなギャップがあることを示しています。
5. 関連研究
FrontierMathは、過去のベンチマークの限界を克服するために設計されており、未発表の新しい問題を用いることでデータ汚染のリスクを排除し、高度な数学的問題を扱うことで難易度を増しています。
6. 数学者とのインタビュー
著名な数学者へのインタビューを通じて、FrontierMathの難易度や意義についての専門家の意見が集められました。問題解決には深い専門知識と時間が要求されるとの評価が一致しています。
7. 考察
FrontierMathはAIシステムの数学的能力を測定する新しい基準を提供します。今後のAIの進展がこのベンチマークに与える影響は重要な課題です。
8. 今後の課題
今後は、FrontierMathの発展に向けて新しい問題を追加し、質の保証プロセスを強化する予定です。また、AIの数学的能力をより良く評価するための多様な評価方法も検討されます。
付録
A. サンプル問題と解答
付録には、FrontierMathの問題のサンプルとその解答が示され、異なる難易度の問題が整理されています。
B. 評価
評価に使用されたモデルの反応やトークン使用量の解析が行われ、AIの問題解決能力に関する詳細が提供されています。
このようにFrontierMathは、AIの数学的推論能力を評価するための新しい基準となり、今後の研究や実用化に向けた重要なステップを踏み出しています。